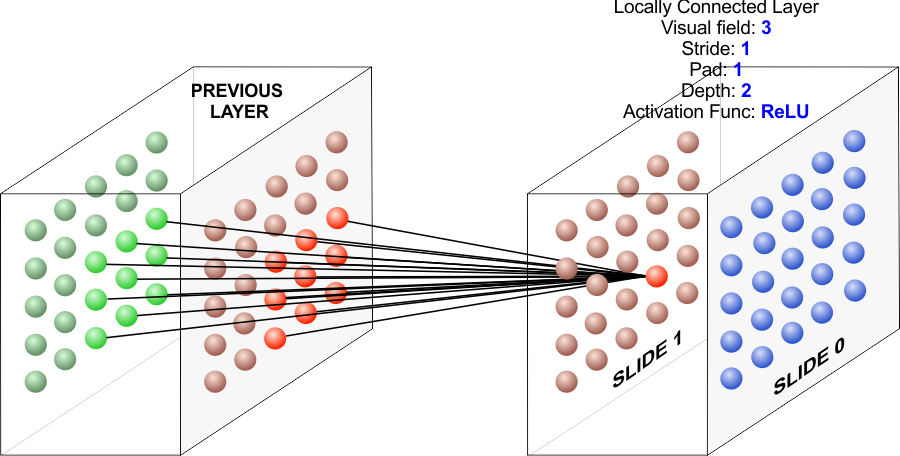
A Locally Connected Layer |
| Locally connected layers were designed to reduce the number of weights used in a fully connected layer. Thus, a locally connected layer is very similar to a fully connected layer. However, only the outputs of the previous layer that are in "the vicinity" are used to compute the activation of the neuron as shown in the figure. Las capas localmente conectadas fueron diseñadas para reducir el número de pesos usados en una capa completamente conectada. Así, una capa localmente conectada es muy similar a una capa completamente conectada. Sin embargo, solamente las salidas de la capa previa que están en "la vecindad" son usadas para calcular la activación de la neurona cómo se muestra en la figura. |
| Tip |
| In a convolutional layer, the filter is the same for all output neurons. In an locally connected Layer, each neuron has its own filter, and therefore, the network can learn different types of feature in different regions of the input. However, the number of weights will be multiplied by the number of output neurons. This will drastically increase the number of weights, and if there is not enough data, it is easy to get over-fitting. En una capa convolucional, el filtro es el mismo para todas las neuronas de salida. En una capa localmente conectada, cada neurona tiene su propio filtro, y por lo tanto, la red puede aprender diferentes tipos de características en diferentes regiones de la entrada. Sin embargo, el número de pesos se multiplicará por el número de neuronas de salida. Esto incrementará drásticamente el número de pesos, y si no hay suficientes datos, es fácil obtener el sobre ajuste. |
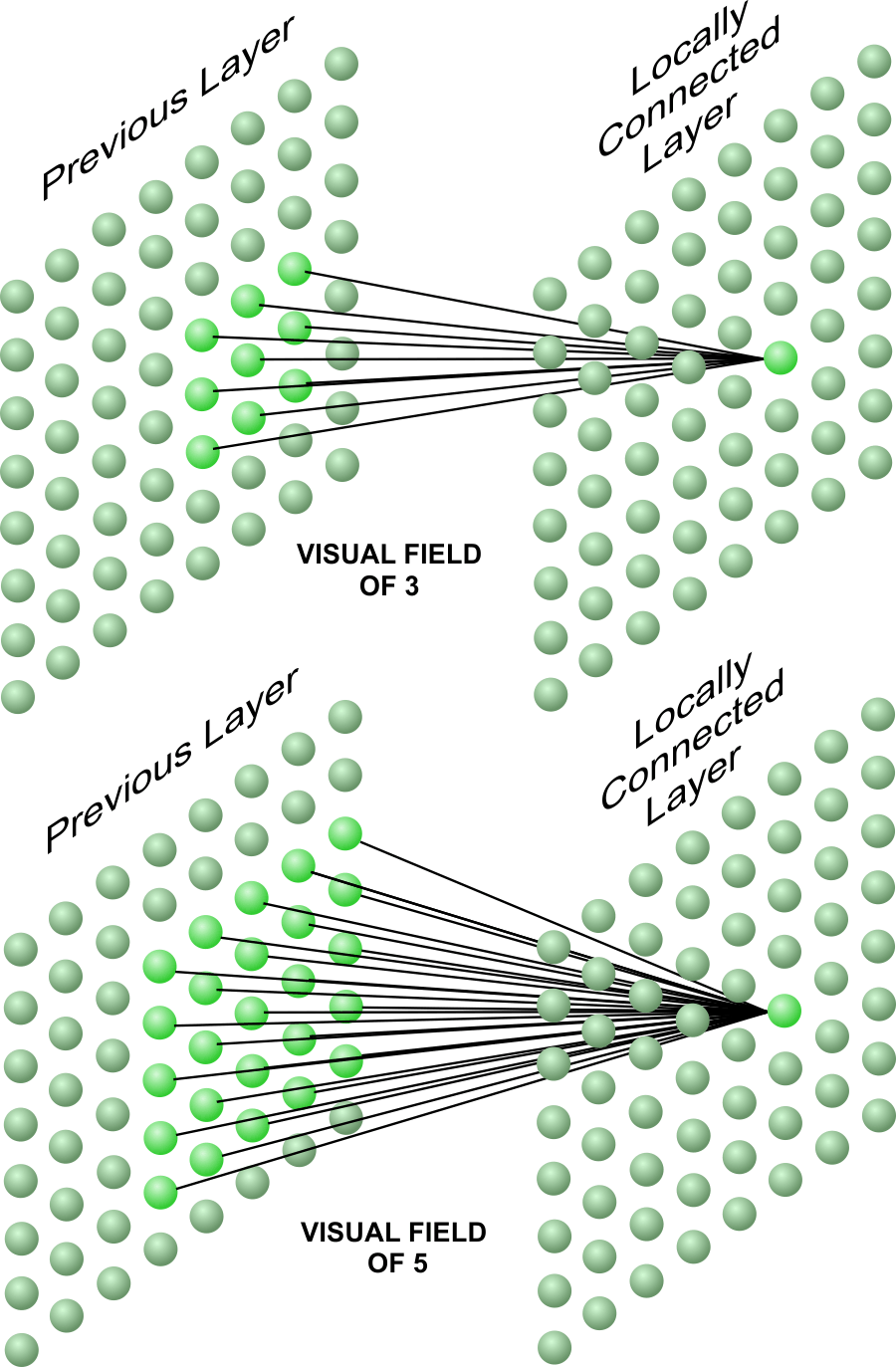
Receptive Field or Visual Field |
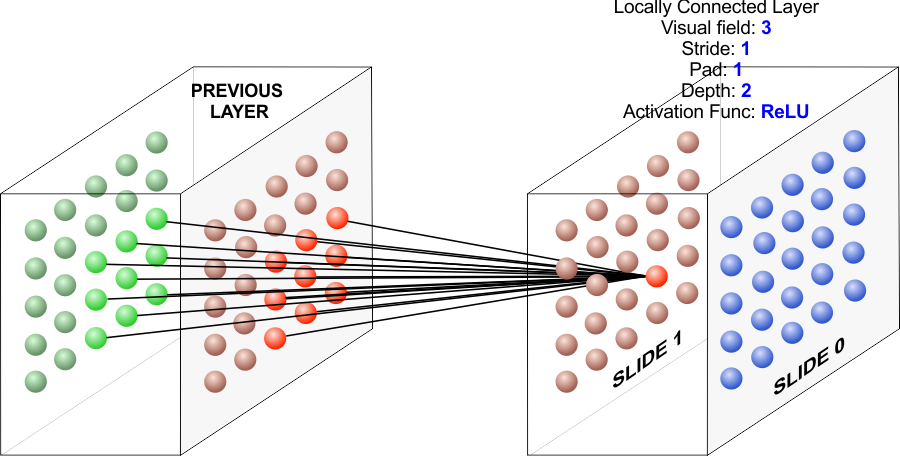
| The visual field indicates the number of outputs horizontally (or vertically) in the previous layer that are used to compute the activation of the current layer as shown in the figure below. In the layer at the top, the receptive field is three because the values in three columns and three rows are used compute the activation of the current layer. In the locally connected layer at the bottom, the receptive field is five. Observe that when the receptive size increases, the number of weights also increases and, consequently training may be come more difficult. El campo visual indica el número de salidas a lo largo (o a lo alto) en el nivel anterior que son usadas para calcular la activación del nivel actual cómo se muestra en la figura de abajo. En la capa de arriba, el campo receptivo es tres porque los valores en tres columnas y en tres renglones son usados para calcular la activación del nivel actual. En la capa localmente conectada de abajo, el campo receptivo es cinco. Observe que cuando el tamaño del campo receptivo se incrementa, el número de pesos también se incrementa y, consecuentemente el entrenamiento puede ser más difícil. |
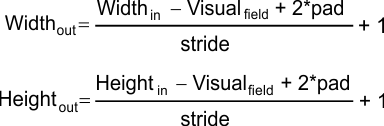
Layer input size and Layer output size |
| The following formulas can be used to compute the width and height of the output tensor using the width and height of the input tensor. Las fórmulas siguientes pueden usarse para calcular el ancho y el alto del tensor de salida usando el ancho y el alto del tensor de entrada. |
| Problem 1 |
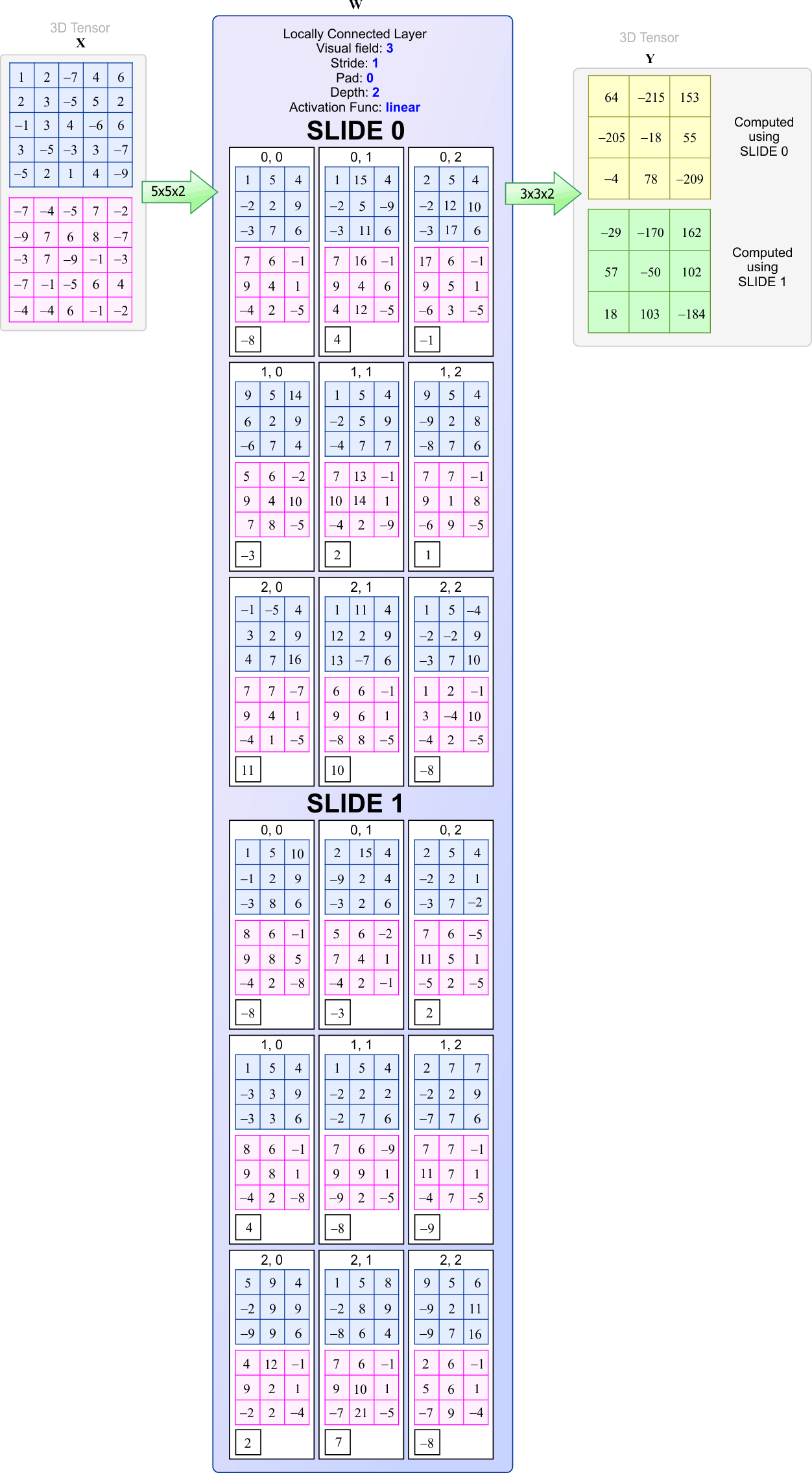
| The figure below shows a locally connected layer with a depth of two. Consequently, there are two slides of neurons: slide 0 and slide 1. Each slide has 3×3 neurons, and each neuron has its own set of weights (19 weights in this case). Thus, the total number of weights in the layer is 19×18. Compute manually the first two output values in slide 0 (64 and −215). La figura de abajo muestra una capa localmente conectada con una profundidad de dos. Consecuentemente, hay dos rebanadas de neuronas: rebanada 0 y rebanada 1. Cada rebanada tiene 3×3 neuronas, y cada neurona tiene su propio conjunto de pesos (18 pesos en este caso). Así, el número total de pesos en la capa es 19×18. Calcule manualmente los dos primeros valores de salida en la rebanada 0 (64 y −215). |
| Problem 2 |
| Can a locally connected network change the depth of the tensor? Explain your answer. Puede una red localmente conectada cambiar la profundidad del tensor? Explique su respuesta. |
| Problem 3 |
| Is vertical and horizontal information preserve when travels through a locally connected layer? Explain your answer. Es la información vertical y horizontal preservada cuando atraviesa una capa localmente conectada? Explique su respuesta. |
| Problem 4 |
The locally connected layer in the figure has a receptive field of three. If each neuron in the current layer is connected to nine neurons in the previous layer and the padding is changed to zero, compute
La capa localmente conectada de la figura tiene un campo receptivo de tres. Si cada neurona en la capa corriente está conectada a nueve neuronas en la capa anterior y el relleno se cambia a cero, calcule
|
| Problem 5 |
| Do you recommend to use a locally connected layer after a fully connected layer? Explain your answer. Recomienda usted usar una capa localmente conectada después de una capa completamente conectada? Explique su respuesta. |